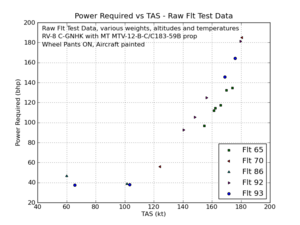
I've gathered cruise performance data on several flights since the aircraft was painted. I've flown at various weights, altitudes and temperatures, so the raw Power Required vs TAS is a bit of a mess.
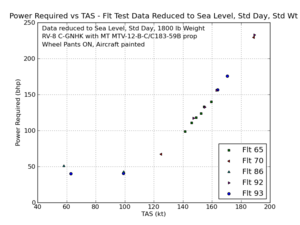 I corrected all the test points to standard conditions (sea level, 15 deg C temperature and 1800 lb weight). The corrected data now starts to show a nice trend of Power Required vs TAS.
I corrected all the test points to standard conditions (sea level, 15 deg C temperature and 1800 lb weight). The corrected data now starts to show a nice trend of Power Required vs TAS.
The classical equation for power required vs speed for propeller-driven aircraft can be transformed so the vast majority of points should fall on a straight line. If you plot power required times speed vs speed to the fourth power, the data should make a nice straight line except for points very close to the stall, or at higher Mach numbers. The drag increases significantly just before the stall due to airflow separation, and it also increases at higher Mach numbers due to wave drag. Note: this analysis assumes the propeller efficiency is constant. This is certainly not true, but it is a very useful simplification, and the evidence from my testing seems to show that the results are still reasonably accurate.
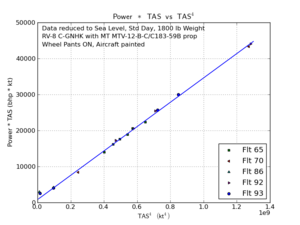 The RV-8 is sadly incapable of Mach numbers where wave drag would be a factor. But, I think the data shows some drag increase at speeds close to the stall. The slowest speed on this plot was extremely close to the stall. The IAS was about 6 kt below the IAS for stall with power off, but the engine was running at medium power to hold level flight, and the prop wash kept the inboard wing (where the stall normally starts) flying. I was on the ragged edge of stall buffet, which means I must have been about one knot above the stall. The next slowest point was a bit further from the stall, but still seems to show a drag increase above the straight line fit through the other points.
The RV-8 is sadly incapable of Mach numbers where wave drag would be a factor. But, I think the data shows some drag increase at speeds close to the stall. The slowest speed on this plot was extremely close to the stall. The IAS was about 6 kt below the IAS for stall with power off, but the engine was running at medium power to hold level flight, and the prop wash kept the inboard wing (where the stall normally starts) flying. I was on the ragged edge of stall buffet, which means I must have been about one knot above the stall. The next slowest point was a bit further from the stall, but still seems to show a drag increase above the straight line fit through the other points.
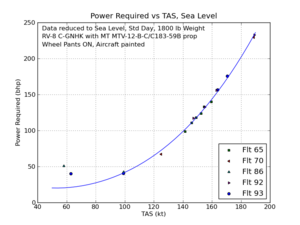 I took the equation for the straight line through the power required times speed vs speed to the fourth power points, and transformed it back into power vs speed.
I took the equation for the straight line through the power required times speed vs speed to the fourth power points, and transformed it back into power vs speed.
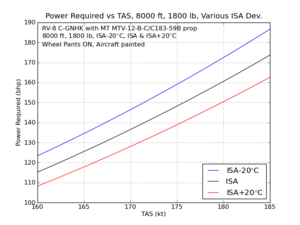 I then corrected this to get predicted performance at 1800 lb weight at 8000 ft at various temperatures.
I then corrected this to get predicted performance at 1800 lb weight at 8000 ft at various temperatures.
I did a tiny bit of cruise performance testing with the original Hartzell prop before I trashed it in the overspeed event. The results of that testing showed that the speed at 75% power at 8000 ft was within a knot of Van's advertised performance. But, I lost about five knots when I switched to this MT prop. Oh well. I can cruise close to 180 kt if I want to burn 12 gph of fuel with mixture set for best power. Fuel is expensive, so I usually cruise between 160 and 165 kt, burning between 8.0 and 8.5 gph running with mixture lean of peak EGT. Not bad.
I'm working on a couple more articles for Kitplanes magazine - one on determining engine power, and cruise performance testing. I've finally got enough data to convince me that the engine power determination and cruise performance methods are working well, so I'll finish off those articles soon.